고정 헤더 영역
상세 컨텐츠
본문

난이도
문제
N개의 선분들이 2차원 평면상에 주어져 있다. 선분은 양 끝점의 x, y 좌표로 표현이 된다.
두 선분이 서로 만나는 경우에, 두 선분은 같은 그룹에 속한다고 정의하며, 그룹의 크기는 그 그룹에 속한 선분의 개수로 정의한다. 두 선분이 만난다는 것은 선분의 끝점을 스치듯이 만나는 경우도 포함하는 것으로 한다.
N개의 선분들이 주어졌을 때, 이 선분들은 총 몇 개의 그룹으로 되어 있을까? 또, 가장 크기가 큰 그룹에 속한 선분의 개수는 몇 개일까? 이 두 가지를 구하는 프로그램을 작성해 보자.
입력
첫째 줄에 N(1 ≤ N ≤ 3,000)이 주어진다. 둘째 줄부터 N+1번째 줄에는 양 끝점의 좌표가 x1, y1, x2, y2의 순서로 주어진다. 각 좌표의 절댓값은 5,000을 넘지 않으며, 입력되는 좌표 사이에는 빈칸이 하나 있다.
출력
첫째 줄에 그룹의 수를, 둘째 줄에 가장 크기가 큰 그룹에 속한 선분의 개수를 출력한다.
예제
| 입력 | 출력 |
|---|---|
| 3 1 1 2 3 2 1 0 0 1 0 1 1 |
1 3 |
| 3 -1 -1 1 1 -2 -2 2 2 0 1 -1 0 |
2 2 |
풀이
우선 이 문제를 풀기 위해서는 CCW 알고리즘을 알아야 한다.
선분 교차 알고리즘인 CCW(CounterClockWise) 알고리즘을 이용한다.
좌표 평면 위의 점 세개를 이용하여 각 선분이 교차 하는지, 평행한지, 교차 하지 않는지를 판단할 수 있다.
선분 $\overrightarrow{AB}$ 와 선분 $\overrightarrow{CD}$ 가 있을 때,
점 $A$, 점 $B$, 점 $C$ 를 이었을 때 반시계 방향인 경우, 시계 방향인 경우, 평행한 경우로 나뉘어진다.
이것을 CCW 알고리즘에서 삼각형 면적 구하는 공식 + 벡터를 이용하여 구한다.
$$
2 \times S =
\begin{pmatrix}
x_1 & y_1 & 1 \
x_2 & y_1 & 1 \
x_3 & y_1 & 3
\end{pmatrix} = (x_2 - x_1)(y_3 - y_1) - (y_2 - y_1)(x_3 - x_1)
$$
의 공식으로 구할 수 있으며
- 0 보다 큰 경우 시계 방향
- 0 보다 작은 경우 반시계 방향
- 0인 경우 평행
로 판단한다.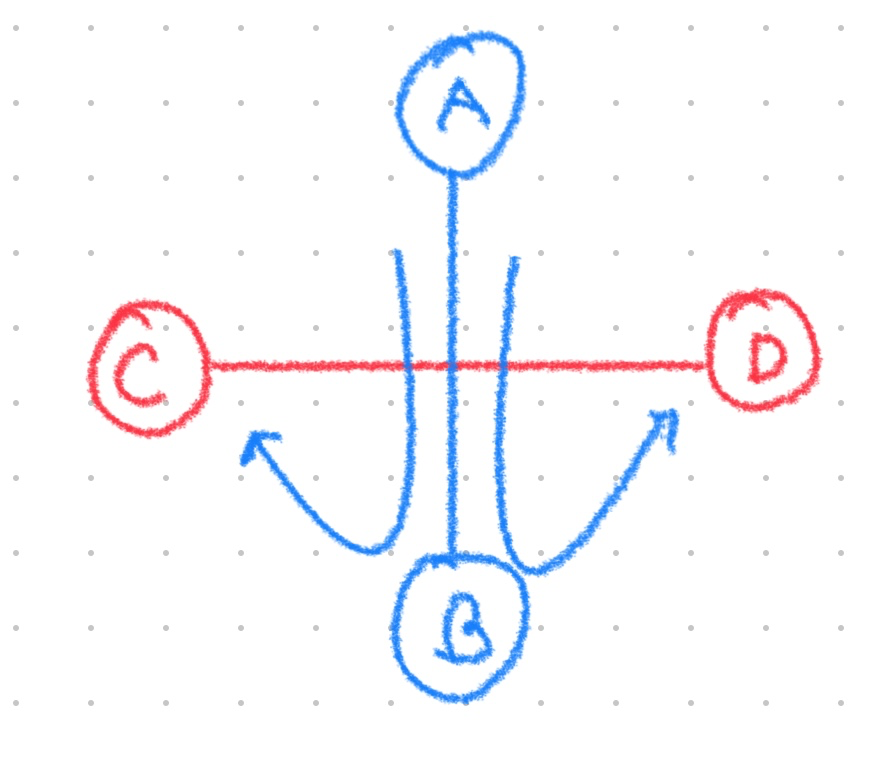
만약 점 A, B, C가 반시계 방향이고, 점 A, B, D가 시계 방향 이라면 서로 교차한다.
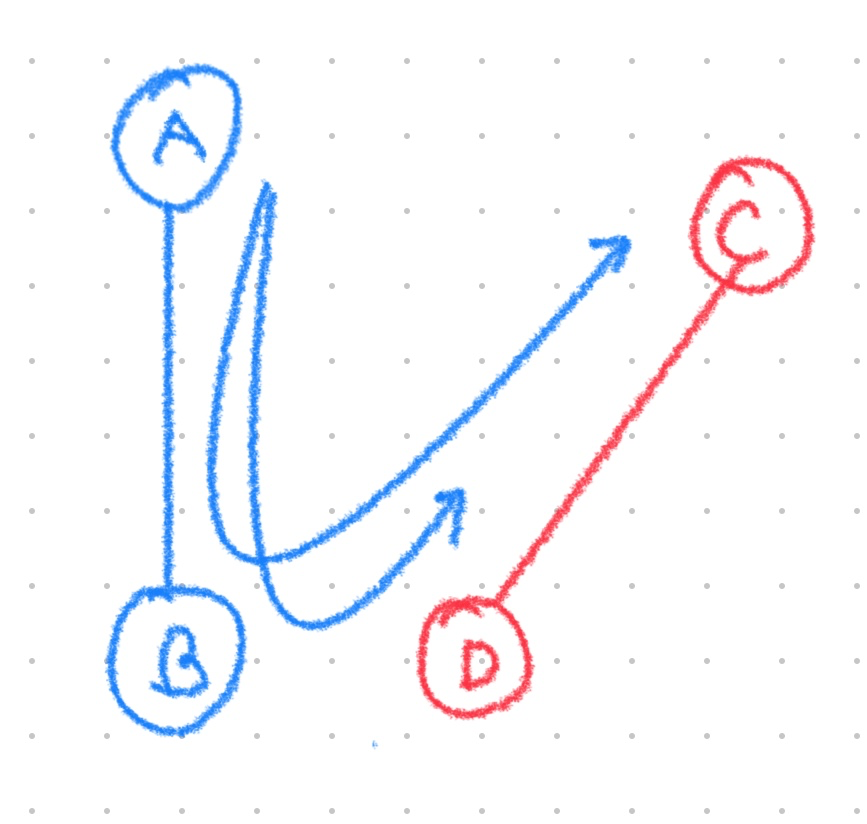
만약 점 A, B, C 가 반시계 방향이고, 점 A, B, D 가 반시계 방향이라면 서로 교차하지 않는다.
즉, 각 점들을 CCW한 값의 곱이 음수라면 교차하고, 양수라면 교차하지 않는다.
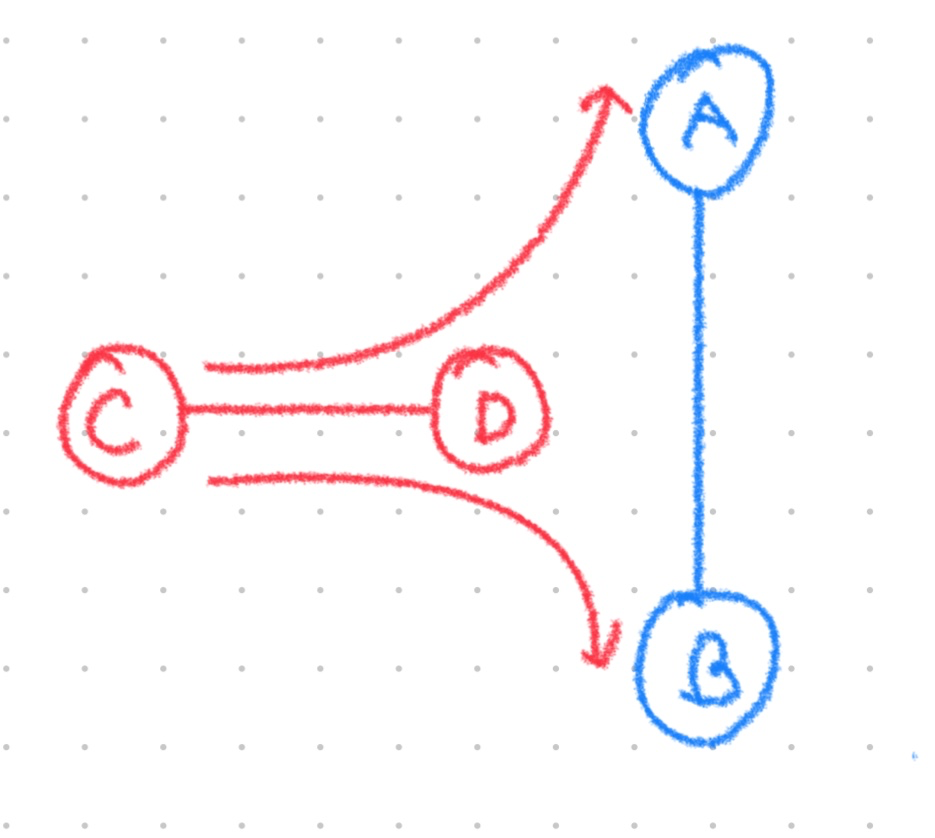
단, 좌표 평면상에서는 CCW 곱의 값이 음수인 경우가 존재하지만 교차하지 않는 경우가 발생할 수 있다.
그러므로 좌표 평면 상에서 교차 여부를 알기 위해서, 점 A, B, C, D를 모두 검사한다.
CCW(A, B, C) * CCW(A, B, D) 도 음수이고, CCW(C, D, A) * CCW(C, D, B) 도 음수인 경우를 찾아야한다.
단, 모든 점이 평행할 때 교차 여부를 판단하려면 점 A, B를, 점 C, D를 작은 점에서 출발 할 수 있도록 상대 위치를 변경해준다.
그리고 해당 문제에서 요구하는 교차하는 선분의 집합과 해당 집합 속 선분의 개수를 알기 위해서, 유니온 파인드 알고리즘으로 집합을 구하고 같은 집합에 속한 선분을 구한다.
유의할 점은 교차하는 중 유니온 파인드를 수행하고 마지막으로 한번 더 유니온 파인드를 수행하여 집합을 압축시킨다.
코드
from sys import stdin
from collections import Counter
input = stdin.readline
N = int(input())
def find(A, root):
if A == root[A]:
return A
else:
root[A] = find(root[A], root)
return root[A]
def union(A, B, root):
A = find(A, root)
B = find(B, root)
if A < B:
root[B] = A
else:
root[A] = B
def CCW(P1, P2, P3):
x1, y1 = P1
x2, y2 = P2
x3, y3 = P3
S = (x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1)
if S > 0:
return 1
elif S < 0:
return -1
else:
return 0
points = []
root = [i for i in range(N)]
for _ in range(N):
x1, y1, x2, y2 = map(int, input().split())
points.append([(x1, y1), (x2, y2)])
for i in range(N):
A, B = points[i]
for j in range(N):
if i == j:
continue
cross = False
C, D = points[j]
ABC = CCW(A, B, C)
ABD = CCW(A, B, D)
CDA = CCW(C, D, A)
CDB = CCW(C, D, B)
if ABC * ABD <= 0 and CDA * CDB <= 0:
if ABC * ABD == 0 and CDA * CDB == 0:
if A > B:
temp = B
B = A
A = temp
if C > D:
temp = C
C = D
D = temp
if C <= B and A <= D:
cross = True
else:
cross = True
if cross:
union(i, j, root)
for i in range(N):
root[i] = find(i, root)
counter = Counter(root)
print(len(counter))
print(counter.most_common()[0][1])
'코딩테스트' 카테고리의 다른 글
| [ 백준 / Python ] S5. 11723 - 집합 (0) | 2024.03.28 |
|---|---|
| [ 카카오 / Python ] 2021 KAKAO BLIND RECRUITMENT - 메뉴 리뉴얼 (1) | 2024.03.23 |
| [ 카카오 / Python ] 2021 KAKAO BLIND RECRUITMENT - 순위 검색 (0) | 2024.03.23 |
| [ 카카오 / Python ] 2022 KAKAO BLIND RECRUITMENT - 양궁대회 (1) | 2024.03.23 |
| [ 카카오 / Python ] 2021 KAKAO BLIND RECRUITMENT - 신규 아이디 추천 (1) | 2024.03.23 |





